时间复杂度和online algorithm (W1)
算法分析中我们常用到三个符号:O,Ω(Omega) 和 Θ(Theta)
- O表示的是渐进上界,它描述了算法在最坏情况下的时间复杂度,表示算法在最坏情况下所需的时间不会超过O的函数。
- Ω表示渐进下界,它描述了算法在最好情况下的时间复杂度,表示算法在最好情况下所需的时间不会低于Ω的函数。
- Θ,描述了算法的时间复杂度的渐进上界和下界,表示算法的时间复杂度在最好和最坏情况下的增长速度是相同的。
在线算法指的是,算法必须在输入数据不是完全可知的情况下,完成相应的计算并输出计算结果。
与之对应的是离线算法,它充分利用了输入数据之间完整的关联特性,即算法运行前所有输入数据均是已知的。
竞争分析针对的是在线算法,已知一个在线算法A,S是问题的一个变量输入序列,用cost(A, S)记录算法A应对S所产生的成本,用cost(OPT, S)记录最优离线算法应对S所产生的费用。若对于任意S都有cost(A, S)<a*cost(OPT, S),则A是一个a-竞争算法。
BST和其他搜索树 (W2)
链表
双向链表,如下图所示,每个节点都有一个前继(prev)和一个后驱(next)。
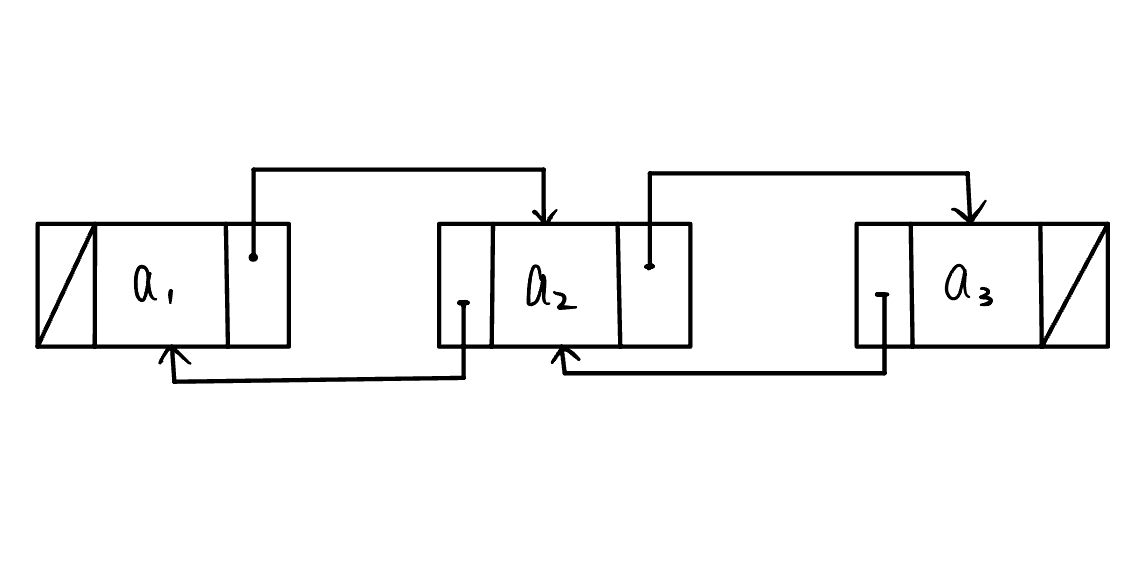
双向链表的几个常用方法
replaceElement(p,e) // p - position, e - element.
swapElements(p,q) // p,q - positions.
insertFirst(e) // e - element.
insertLast(e) // e - element.
insertBefore(p,e) // p - position, e - element.
insertAfter(p,e) // p - position, e - element.
remove(p) // p - position.
介绍其中一个方法:insertBefore()
技巧:要确保每个节点的前后两个指针都有连接,如上图所示。
s.prev = p; /* 把 p 赋值给 s 的前驱 */
s.next = p.next; /* 把 p->next 赋值给 s 的后继 */
(p.next).prev = s; /* 把 s 赋值给 p->next 的前驱 */
p.next = s; /* 把 s 赋值给 p 的后继 */
List更新的复杂度分析(remove和insert)
- 如果元素p的位置已知,则复杂度为O(1)
- 如果只知道list的头,则复杂度为O(p),因为需要遍历list来找到p
二分查找(BST)
一个有序数组通常称为lookup table。
- 输入一个有序数组
- 输出要查找的值及其对应的key
BINARYSEARCH(S,k ,low ,high)
if low>high
return no_such_key
else
mid = Math.floor((low+high)/2)
if k = key(mid)
return elem(mid)
else if k<key(mid)
return BINARYSEARCH(S, k, low, mid-1)
else
return BINARYSEARCH(S, k, mid+1, high)
- key (i): the key at index i
- elem(i): the element at index i
lookup table 和 linked list比较
| Method | LinkedList | lookup table |
|---|---|---|
| 查找元素 | O(n) | O(logn) |
| 插入元素(已知位置) | O(1) | O(n) |
| 移除元素 | O(n) | O(n) |
| ClosestKeyBefore | O(n) | O(logn) |
有没有一种数据结构可以既保证查找的效率又保证插入的效率?(综合lookup和linkedlist的优点) — BST maybe possible.
- 二叉树的节点深度:节点的祖先的数量(排除节点自己)
- 二叉树的高度=该树最大的节点深度
二叉树的遍历方法
- 前序遍历(pre-order)
- 中序遍历(in-order)
- 后序遍历(post-order)
所有的BST的操作的时间复杂度都是O(h),h表示树的高度。如果情况糟糕的话,h很有可能等于n(对于一个degenerate tree来说)。 如果BST不平衡的话,它最差的搜索时间可能是O(n),这就失去了它的优点。
因此我们衍生出一种具有高度平衡的性质的树——AVL树
AVL树
AVL树的性质:对于树T中的每个内部节点v,v的子节点之间的高度差最多是1。
存储n个节点的AVL树的高度是O(logn)
证明:一个高度为h的AVL树,令这棵树的内部节点最少有$n_h$个。最坏情况下,左树的高度为h-1,右树高度为h-2,且两颗子树都是AVL树。
所以$n_h = n_{h-1} + n_{h-2} + 1$,意思是整个树的节点是由左右两颗子树的节点加上根节点,因为$n_{h-1} > n_{h-2}$,所以$n_h>2\times n_{h-1}$ -> $n_h>2^{{h\over 2}-1}$
- AVL树中的搜索操作,时间复杂度为O(logn)
- AVL中的插入和移除操作要小心(要使用rotation来保证height balance)
旋转这个操作太麻烦,在b站找到一个宝藏嚣张教程,记录一下。
宗旨:自下而上地找最小的一颗不平衡子树,如果向上找的节点太多,就选择离根节点最近的三个节点(包括根节点),将三个节点拿出来树状排序,插入原来的位置。剩下的元素根据二叉树的规则重新插入。
在下面这个AVL树中插入90
插入后效果如下
(2,4)树
(2,4)树的定义是这棵树的子节点,最少有两个,最多有四个。每个内部节点都包含1-3个键,这些键定义了存储在子树中的键的范围。这样的键要保证,比它最左边的子树中最大的键大,比最右边的子树中最小的键小。
(2,4)树的所有叶子节点都具备相同的深度。
- n个元素存储在(2,4)树中,其高度为O(logn)
- 拆分,转移和融合操作花费O(1)的时间
- 搜索,插入和删除元素需要访问树中O(logn)个节点。
排序-Sorting(W3)
排序问题,给一个集合C,包含n个元素,将C中的元素以升序方式重新排列。
排序通常是解决问题过程中的一个子例程。也就是说,想要实现算法的良好性能,高效的排序是很有必要的。
Priority Queues
优先队列是一个存储元素的容器,每个元素都有对应的key。
优先队列的基本方法:
- insertItem(k, e)
- removeMin()
- minElement()
- minKey()
使用优先队列对一个集合C进行排序分为以下两个步骤
- 首先使用insertItem(k, e),将C中的元素都放在优先队列P中。
- 使用removeMin()方法以升序方式从P中提取元素。
堆
堆是一种完全二叉树,即除了最后一层外,其它层都是满的,最后一层从左到右填满。n个元素的高度的是O(logn)
堆是有效的优先队列的实现,在插入元素和删除元素方面,堆允许在log时间内插入和删除元素。
在堆中,元素和键都被存在二叉树中。子节点中元素的键要大于等于其父节点中的键(堆序性-最小堆)
堆插入
堆中的插入操作,需要维护堆序性
- 将要插入的元素放在堆的底部(最后一个叶子节点的右侧)
- 比较该元素与其父节点的值,如果该元素的值小于(最小堆)其父节点的值,则交换这两个节点,然后继续向上比较(这个过程和bubble类似),直到满足堆序性为止。
- 插入操作完成后,堆中会多出一个元素,需要将堆的大小加 1。(堆的大小=堆中元素数量)
堆删除
堆中的删除操作,同样需要维护堆序性
- 取出堆顶元素
- 将最后一个叶子节点的值赋给堆顶元素。将最后一个叶子节点的值放到堆顶,相当于将堆顶元素删除,同时保证了堆仍然是一棵完全二叉树。
- 对新的堆顶元素进行下滤操作。下滤的过程类似于插入操作,将新的堆顶元素与它的子节点比较,如果子节点中有比它更小的,则交换位置,直到找不到比它小的为止。
| Operation | time |
|---|---|
| size,isEmpty | O(1) |
| minElement,minKey | O(1) |
| insertItem | O(logn) |
| removeMin | O(logn) |
堆排序
- 从下到上构造一个有n个元素的堆,时间复杂度为O(nlogn)
- 升序提取n个元素的时间复杂度为O(nlogn)
分治(Divide and Conquer)
顾名思义了,把一个大问题拆分,解决子问题后,再进行合并。(Divide-Recur-Conquer)
归并排序(MergeSort)
分治的经典例子,mergesort
对mergesort的divide部分,很好理解,但是到了merge部分就有些懵懂,因为有些课程省略了步骤,现在记录一下详细步骤。
假设到了合并这一步,现在有两个数组arr1和arr2
arr1 = [2, 5, 7, 8]
arr2 = [1, 3, 6, 9]
我们要将它们合并成一个有序数组。首先,我们需要开辟一个长度为len(arr1) + len(arr2)的临时数组temp
接下来,需要设置两个指针i和j,分别指向两个数组的第一个元素,用于比较两个数组中的元素。还需要一个指针k,指向临时数组的第一个位置,用于存储排序后的元素。
时间复杂度分析
n个元素进行mergesort的时间复杂度为O(nlogn)
将mergesort的过程理解为二叉树,那么这颗二叉树的高度为O(logn)。这颗二叉树中每个子节点的复杂度为O(n),因为要进行排序,最坏情况下,每个元素都会被访问一次。因此时间复杂度为O(nlogn)。空间复杂度为O(n),因为需要另开辟一个长度为n的数组,存储排序好的数据。
Counting inversions
长话短说,一组序列,有一对数i和j,都有i<j, 而且a[i]>a[j],则称(i, j)是一个逆序对,Counting inversions就是一种计算逆序对数量的算法。
最笨的解决办法:找出所有数对并一个一个查看。这样做的时间复杂度是O(n^2),太贵,做不起。
使用分治,可以把时间复杂度压缩到O(nlogn)
具体做法
- 将一个序列按照中间位置分为左右两个子序列,递归地对左右两个子序列进行排序,并计算它们内部的逆序对数。
- 将左右两个子序列合并为一个有序的序列,同时计算左右两个子序列之间的逆序对数。
- 返回左右两个子序列内部的逆序对数、左右两个子序列之间的逆序对数以及合并后的有序序列。
- 逆序对数=两个子序列内部的逆序对数 + 左右两个子序列之间的逆序对数
时间复杂度分析
- 因为需要遍历两个子序列中的所有元素,因此复杂度是O(n),n是序列中元素的数量。
- 由于每次递归的时候,问题规模减半,因此归并排序需要递归 logn 层
- 每层的复杂度是O(n),因此归并排序时间复杂度是O(nlogn)
快排(QuickSort)
快排也是分治算法的一种,但是这种排序方法不同于归并排序。
基本思想:随机选择一个基准元素(pivot element),然后将数组分为两个子序列,小于基准元素的放在左边,大于基准元素的放在右边,然后递归地对两部分排序,知道序列变得有序。
具体过程
- 选择一个基准元素(pivot),可以选择第一个元素、最后一个元素、中间的元素或者随机选择。
- 从序列的两端开始向中间扫描,左端找到一个比基准元素大的数,右端找到一个比基准元素小的数,交换这两个数的位置。
- 继续扫描,直到左右两个端点相遇。此时,所有比基准元素小的数都在基准元素的左边,比基准元素大的数都在基准元素的右边。
- 递归地对左右两个子序列进行快速排序。
- 当序列中只剩下一个元素时,排序结束。
时间复杂度分析 最坏情况下,每次划分都只能将序列分成一个元素和 n - 1 个元素两部分,这种情况下递归树的深度为 n,每层的时间复杂度是 O(n)(因为需要遍历所有 n 个元素进行比较)。因此,最坏情况下的时间复杂度为 O($n^2$)。
在最好情况下,每次划分都将序列分成长度相等的两部分,这种情况下递归树的深度为 log(n),每层的时间复杂度是 O(n)。因此,最好情况下的时间复杂度为 O(n log n)。
如何避免worst case? 随机选择pivot。随即快排的期望运行时间是O(nlogn)
如果分割的两部分的长度都不大于序列长度的3/4,则这样的pivot就是好的随机pivot。所以成功选择一个好的随机pivot的概率是1/2
线性时间排序(Bucket Sorting)
桶排序就是将数据分到不同的桶里,然后对每个桶中的数据进行排序,最后把所有桶中的数据合并起来得到有序序列
具体过程
- 将待排序的数据分配到不同的桶中。
- 对每个桶中的数据进行排序,可以选择任意一种排序算法,比如插入排序、归并排序等。
- 将各个桶中的数据按照顺序合并起来,得到有序序列。
桶排序适用于数据分布比较均匀的场景,如果数据分布不均匀,有些桶的数据量会比较大,就会影响桶排序的效率。比如对成绩进行排序,可以将分数分为 0-59、60-69、70-79、80-89、90-100 等五个区间,分别放到对应的桶中进行排序。
基数排序(Radix Sorting)
这是一种非比较排序算法,它是根据每个位的值来进行排序的。 在每一列上进行桶排序,然后逐列进行排序。可以将待排序的数据按照位数的不同,将其分配到不同的桶中进行排序,最后将所有桶中的数据按顺序合并起来。
时间复杂度分析
基数排序的时间复杂度取决于每次排序的子排序算法
- 如果使用插入排序作为子排序算法,基数排序的时间复杂度为 O($d\cdot(n+k)$),其中 d 表示待排序数据的位数,n 表示待排序数据的个数,k 表示桶的个数。
- 如果使用quicksort或mergesort作为子排序算法,基数排序的时间复杂度可以降低到 O($d\cdot n$),但是空间复杂度会略有增加。
细说分治(W4)
我们通常使用递归来分析分治算法的运行时间。
当输入数据的大小为n时,使用T(n)来表示运行时间。
以Mergesort为例
- T(n) = c if n$<$2
- T(n) = 2$\times$T(n/2) + cn if n$\ge$2
c是一个常数,表示合并当前层的两个子列表时需要做多少次比较或移动操作,因为具体计算c的大小与具体的算法有关,所以只用一个常数来表示,cn的时间复杂度就是O(n)。2$\times$T(n/2) 表示递归排序2个子序列的时间复杂度。
分治的递归表达式
- T(n) = c if n$\le$d
- T(n) = aT(n/b) + f(n) if n$>$d
表达式中,a表示每次递归需要解决的子问题的数量,b表示子问题的规模,f(n)表示非递归部分的时间复杂度。
举个例子$T(n) = 3T(n/2) + n^2$ 。这个递归式的意思是将一个规模为 n 的问题分成 3 个规模为 n/2 的子问题来解决,然后再用 O($n^2$) 的时间将这些子问题的解合并起来得到原问题的解。
主定理(Master Method)

- 第一种情况,表示子问题的时间复杂度是主要因素,即时间复杂度主要是子问题说了算。
- 第二种情况,表示子问题规模与原问题规模相等,如果我们可以将原问题分成几个大小相等的子问题,并且解决每个子问题的复杂度相同。例如mergesort。
- 第三种情况,表示子问题规模对主问题的时间复杂度影响很小,主要由f(n)决定。
整数快速乘法(Fast multiplication of integers)
当有两个非常大的整数相乘(位数很多),其时间复杂度是O(n^2),因为数字中的每一位都要和另一个数的所有位进行乘法操作。快速整数乘法就是找出算法来缩小时间复杂度。
Karatsuba Algorithm
利用分治的思想,假设我们要计算两个n位整数x和y的积,x和y可以分别表示为
- $x = a * 10^{n/2} + b$
- $y = c * 10^{n/2} + d$
其中,这里以十进制为例,如果是二进制,把10替换成2就可以。a和c是x和y的高位部分,b和d是它们的低位部分
因此,$xy=ac \cdot 10^n + (ad + bc) \cdot 10^{n/2} + bd$。我们可以通过递归计算这些值,并组合起来得到最终结果。由于ad+bc=(a+b)(c+d)-ac-bd,ac和bd用到的是前后已经求出来的值,因此每次只需要被分解成3个子问题即可,即
- 计算ac的值
- 计算bd的值
- 计算(a+b)(c+d)的值
由此,我们可以得出递归表达式为T(n) = 3T(n/2)+cn,即进行了3次乘法计算和6次加减法计算。根据主定理,$cn<log3$,因此这种算法的时间复杂度为$n^{log3}<n^2$,此处log以2为底。
矩阵乘法(Matrix Multiplication)
 根据图中的递归表达式,我们可以得出时间复杂度为O($n^3$),很费钱。
根据图中的递归表达式,我们可以得出时间复杂度为O($n^3$),很费钱。
Strassen’s Algorithm
理解了上面图中的东西,这个算法就很好理解了。这个人找到了一种方法,用更少的步骤就可以解决矩阵乘法。 首先找到7个矩阵乘积
| $S_1$ | $S_2$ | $S_3$ | $S_4$ | $S_5$ | $S_6$ | $S_7$ |
|---|---|---|---|---|---|---|
| a(f-h) | (a+b)h | (c+d)e | d(g-e) | (a+d)(e+h) | (b-d)(g+h) | (c-a)(e+f) |
之后,结果可以用如下式子表示
- $I = S_4 + S_5 + S_6 − S_2$
- $J = S_1 + S_2$
- $K = S_3 + S_4$
- $L = S_1 + S_5 + S_7 − S_3$
因此,递归表达式可以写成
$T (n) = 7T(n/2) + bn^2$
在根据master method可以得出,时间复杂度有所缩小,变成了O($n^{\log_2 7}$)
浅说贪心(W5)
一些广泛应用在不同问题上的算法工具
- 贪心
- 分治
- 动态规划
第一个想到的就应该是贪心。贪心算法能求出解的问题具备greedy-choice的属性。
Greedy-choice property
Greedy-choice property是指每一步所做的贪心选择都能导致局部最优解(即当前情况下最优的解),从而最终得到全局最优解。
可以被贪心算法解决的问题
- Fractional Knapsack Problem
- Interval Scheduling
- Task Scheduling
- Minimum spanning trees
- Shortest Paths
- Change Making
- Maximum Spacing k-clustering
FKP
FKP问题指的是:一个含有n个元素的集合S,S中的每个元素i都有一个正的收益和正的权重。目的是在不超过总权重W的情况下,找到一个具有最大收益的子集。
需要说明的是,这个问题和0/1背包问题不同(每个物品只能选择放或者不放)。FKP可以将物品分成一部分放入背包,而不必完全舍弃。对0/1背包问题,greedy通常不会发现最优解。(动态规划可以
对于分割成的部分,我们将其份数定义为$x_i$,对于所有的元素i,$x_i<w_i$。因此固定总权重下总收益的公式为 $$\sum_{i\in S} b_i(x_i/w_i)$$ 因此我们可以计算每个元素i的价值指数。$v_i = b_i/w_i$。这可以计算出每单位重量的价值,价值指数越高的物品越容易被优先选择。
说到优先选择就会想起优先队列,想到优先队列就会想起堆。把最大的价值指数插在堆的根节点。建造一个堆需要的时间复杂度为O($n\log n$)。每次贪心选择(移走堆中剩下的最大的价值指数)需要O($\log n$)。
因此,给出一个FKP问题,我们都可以构造出一个最大收益的子集在O($n\log n$)时间内。
Interval Scheduling
Interval Scheduling指的问题是,我们有一系列任务在一个集合中。现在只有一个机器去处理这些任务。我们的目的是选择一个调度顺序使得任务的完成数量最大化。
怎么办?找最先开始的任务?那万一这个任务和大部分其他任务都冲突怎么办?那找具有最小时间间隔的两个任务?那和其他任务时间间隔很长怎么办?或者找一个和大部分任务都不冲突的任务?同样无法保证上述问题被解决(没法保证中间有很多不该浪费的时间被浪费)
综合上面的想法,我们发现问题并不是出现在谁先开始,而是如何保证开始后不浪费不该浪费的时间。因此可以想到
把任务按照结束时间进行排序,选择第一个结束的任务作为第一个,然后移除所有和这个任务冲突的任务。然后一直重复这样做,直到集合中为空。这样就可以保证不浪费过多的时间。这个算法的时间复杂度为O($n\log n$)。主要是排序的时间。
Task Scheduling
Interval Scheduling是只用一个机器调用任务,Task Scheduling是可以用几台机器调用任务,目的是求出想处理所有问题,机器的最小使用数量。贪心仍然可以解决这个问题,只不过我们可以考虑用初始时间来排序了。
对于每一个任务i,如果这台机器空闲可以处理,那么就把这个任务分配给这台机器。否则,我们分配一个新机器去处理它。重复这个过程直到所有任务都被处理。
处理n个任务,用最少的机器数量,产生这个调度的时间复杂度为O($n\log n$)
为什么贪心有效?(证明)
假设现在的算法可以找到k个机器来解决问题,突然冒出来个说法说用k-1个机器就可以解决。
假设k是现在的算法分配的最后一个机器。任务i是这台机器上被分配的第一个任务。根据我们的算法来讲,任务i之所以被分配到第k个机器上,是因为剩下k-1台机器上的任务都与任务i冲突。也就是说这些任务都是开始时间在i之前,但是在i之后结束。如果这些任务都是这样,那也说明了他们之间也是两两冲突的。也就是说,集合中有k个任务是两两冲突的,那就不可能用k-1台机器来解决这个问题。因此,贪心给了一个全局最优解。
Clustering
这个问题说白了就是距离问题,有三点规则
- d($p_i, p_i$) = 0, 对于所有的i
- d($p_i, p_j$) = 0, $i\neq j$
- d($p_i, p_j$) = d($p_j, p_i$)
Maximum Spacing Clustering
目的:给n个对象和一个k值,找到具有最大簇间距的k聚类。
已知N个点,给出一对点之间距离的定义(比如欧几里德距离),spacing定义为任意两个属于不同类的点之间距离的最小值,要求聚成k个类,使得spacing最大。类似kruskal算法,将所有边从小到大排序,开始每个点属于1个cluster,然后将距离最小的两个点合并,继续下去,直到只剩下k个cluster。
通过将点分组到簇中,使得每个簇内部的点之间距离的最小值尽可能大,进而使得不同簇之间的最小距离尽可能大。最大化两个cluster之间最近的两个点,才能达到良好的聚类效果(类似放缩思想)。
时间复杂度分析
假设有n个点,已知对n个元素进行排序的时间复杂度为O($n\log n$),但是我们要计算两两点之间的距离并进行排序,因此$n\log n$中的n=$n^2$,所以是$n^2\log n^2 = 2n^2 \log n$。因此时间复杂度为O($n^2\log n$)
聊聊动态规划 (W6)
动态规划的思想和分治比较像,都是将一个大问题拆分成很多子问题来解决。区别是,
- 分治将问题拆开后,求得子问题的解,在解决问题是要合并子问题(重复递归调用)得到最终解。
- 动态规划是将问题拆成若干子问题,求得子问题的解并存储起来,以便下一次需要求解相同的子问题时可以直接使用已经求解过的结果。
当暴力解法不可行的时候,动态规划通常会派上用场。
使用动态规划的常用手段就是先找到问题的递归解,然后存储子问题的解自底向上迭代计算。什么是递归解?斐波那契数列中f(n) = f(n-1) + f(n-2)就是一个递归解。
memoization
正常情况下,动态规划是需要指数级的时间复杂度,因为它需要计算所有情况然后取最优解。但是使用备忘录,将计算过的子问题的解存入数据结构中,不管是数组还是HashMap,这可以避免重复计算相同的子问题,将指数级的时间复杂度降到多项式级别。
0-1背包问题
困扰了我一晚上的问题,终于搞懂了。我主要的误区在于用贪心的思想来看这道动态规划的题目。动态规划就是找出所有可能的情况,然后在这些可能的情况中找出最优解。
- 首先定义状态dp[i][j],意思是前i个物品,在背包剩余重量为j时,可以获得的最大价值。
- 因此状态转移方程可以有如下定义
- 如果要装的第i个物品的重量大于背包的剩余重量j,那么不装这个物品,则dp[i][j] = dp[i-1][j]。
- 如果要装的第i个物品的重量小于背包的剩余重量j,那么可以选择装或不装,两种情况中,价值更大的一种,即$dp[i][j] = max(dp[i-1][j], dp[i-1][j-w_i] + v_i)$。
- 到这里我就有疑问了,既然把东西装进去了,怎么可能比不装这个东西的价值要小?这个max的存在根本就没意义?
- 这是因为,在某些情况下,选择当前物品可能会导致在之后的决策中错过更高价值的物品。
- 问题又来了,那我怎么能在装这个物品的时候知道之后的事情?
我的这个思路就是贪心的思想,总是考虑当前步骤,但实际的动态规划的步骤是这样的
🌰 举个例子,有三个物品123,W=5, w={1,4,3}, v={2,4,7}
当我们考虑物品 2 时,假设我们选择了它。这将导致背包剩余承重为 5-4=1,我们无法再选择物品 3,因为它的重量超过了剩余承重。这种情况下,我们应该选择1,现在背包中物品的总价值为 v1 + v2 = 6。 但是,如果我们不选择物品 2,这将保留足够的空间来容纳物品 3。在这种情况下,背包中物品的总价值为 v1 + v3 = 9,这比选择物品 2 的情况要高。
// i=1 (物品1)
dp[1][0] = max(dp[0][0], dp[0][-1]) = 0
dp[1][1] = max(dp[0][1], dp[0][0] + 2) = 2
dp[1][2] = max(dp[0][2], dp[0][1] + 2) = 2
dp[1][3] = max(dp[0][3], dp[0][2] + 2) = 2
dp[1][4] = max(dp[0][4], dp[0][3] + 2) = 2
dp[1][5] = max(dp[0][5], dp[0][4] + 2) = 2
// i=2 (物品2)
dp[2][0] = max(dp[1][0], dp[1][-4]) = 0
dp[2][1] = max(dp[1][1], dp[1][-3]) = 2
dp[2][2] = max(dp[1][2], dp[1][-2]) = 2
dp[2][3] = max(dp[1][3], dp[1][-1]) = 2
dp[2][4] = max(dp[1][4], dp[1][0] + 4) = 4
dp[2][5] = max(dp[1][5], dp[1][1] + 4) = 6
// i=3 (物品3)
dp[3][0] = max(dp[2][0], dp[2][-3]) = 0
dp[3][1] = max(dp[2][1], dp[2][-2]) = 2
dp[3][2] = max(dp[2][2], dp[2][-1]) = 2
dp[3][3] = max(dp[2][3], dp[2][0] + 7) = 7
dp[3][4] = max(dp[2][4], dp[2][1] + 7) = 9
dp[3][5] = max(dp[2][5], dp[2][2] + 7) = 9
因此,逻辑应该是两个循环,外面的循环是物品的个数,内部的循环是背包总容量,对于每个物品,都要计算出其在不同剩余容量下所对应的价值。最后才能通过max取到最大值。
Weighted Interval Scheduling
在贪心算法中,有提到过Interval Scheduling,意思是有多个任务,在一台机器上调度,问最多可以调度多少个任务。而Weighted Interval Scheduling,意思是每个任务都带有价值,问如何调度才能使价值最大化。
这个问题用贪心给出的方案很可能不是最优解,需要使用动态规划。
首先我们定义p(j),p(j)表示和任务j不相交,但是最接近的任务i,i<j。
接下来定义状态,对于一个任务n,机器只有两个选择,调度或者不调度。
- 如果调度序列包含n,那么这个序列一定是{1, 2, …, p(n)}
- 如果调度序列不包含n,那么这个序列一定是{1, 2, …, n-1}
然后定义序列$S_j$是对于序列{1, 2, …, j}的最优解,Opt(j)代表$S_j$的值。
- If $j\in S_j$
- $Opt(j) = v_j + Opt(p(j))$
- If $j\notin S_j$
- $Opt(j) = Opt(j-1)$
由此可得,$ Opt(j) = max ({ v_j + Opt(p(j)), Opt(j-1) }) $
为了避免指数级的时间复杂度,先计算出Opt(1)到Opt(n)的值,之后再找Opt(n)的值需要O(nlogn)的时间复杂度
探秘图-最短路径(W7)
Connectivity information
通常是描述一个网络中节点之间连接方式的信息。
Graph
图是一个对象的集合,包括顶点和边。
Some Terminologies
- 一条edge的两个顶点时adjacent的
- 一条edge incident在这个顶点上,如果这个顶点是edge的一个顶点
- 从一个顶点出发的有向边称为outgoing edge,->
- 一个顶点接受的有向边称为incoming edge,<-
- 一个顶点v的degree表示incident在当前顶点上边的数量,记为deg(v)
- 对于有向图,incoming和outgoing的edge,记为indeg(v)和outdeg(v)
Theorem
- 对于有m条边的无向图,$\sum_{v \in V} deg(v) = 2m$
- 对于有m条边的有向图,$\sum_{v \in V} indeg(v) = \sum_{v \in V} outdeg(v) = m$
如果无向图中每一对顶点之间都有边连接,则这个图是简单图,simple graph
如果有向图中每一对顶点之间最多有一条边连接,则这个图是简单图。
spanning subgraph指的是包含图G中所有顶点的子图
spanning tree生成树是一个图的spanning graph,同时还是一颗free tree
如果这个图不是connected,那么图G的最大连接子图叫做图G的connected component。
Connected, tree和forest的关系
- 全连接图是最密集的形式,任意两点都直接相连;
- 树是无环且连通的,边数恰好比节点数少一;
- 森林则是多个树的集合,可能是不连通的。
G是一个有n节点和m条边的无向图
- 如果G是一颗树,m = n-1。
- 数学归纳法证明
- Base case考虑只有一个节点的图,此时它没有边,满足节点数(1)等于边数(0)加一的条件。只有两个节点的树,也满足条件。
- Hypothesis 假设所有具有k个节点的树都满足“节点数等于边数+1”的规则。
- Induction step 现在有一个k+1个节点的树,选择一个叶子节点并移除,剩下的图仍然是一颗树,这棵树满足我们的假设“有k个节点和k-1条边”。然后,将移除的叶子节点和边加回到图中。这样,我们就得到了原始的树,它有k+1个节点和k条边。因此这棵树也满足“m=n+1”的规则
- 数学归纳法证明
- 如果G的边的数量大于节点的数量,即$m\geq n$,那么G中存在cycle。
- 数学归纳法证明
- Base case 考虑节点数为1,2,3。如果想要有环,边的数量一定要大于等于节点数。
- Hypothesis 节点小于k的图中,边的数量大于等于节点数,那么这个图中一定存在环。
- Induction step 现在一个图中有k+1个节点,想要证明当边的数量>=节点数时,这个图中存在环。现在移除图中的一个节点及其所连接的所有边。因为不知道移除的节点附带几条边,所以分成两种情况讨论
- 移除的点的deg=1,移除了一个节点和一条边,那么现在边的数量依然大于等于节点的数量,符合我们的假设。因此k+1个节点时图中必定有环。
- 移除的点的deg>1,移除的这个节点由于连接了多于一条的边,所以在移除它之前,图中必然已经存在环。因此,对于节点数为k+1并且边数大于等于k+1的图,仍然可以确定图中一定存在环。
- 数学归纳法证明
- 如果G中没有cycle,那么$m\leq n-1$
- 上面的反证,没啥好说的了。
- 如果G是connected(连通,注意和全连接的区别),那么$m\geq n-1$
- 数学归纳法证明
- Base case 考虑节点数1,2。都是连通的。
- Hypoithesis 假设节点数量小于或等于k的图,如果边的数量>=节点数量减1,那么图一定是连通的。
- Indection step 现在一个图中有k+1个节点,想要证明当边的数量>=节点数-1时图是连通的(即边的数量为k)。假设当前的图是不连通的,即有至少两个子图。那么当前边的数量一定是小于节点数量-2。这与当前的假设矛盾,因此这个图是连通的。
- 数学归纳法证明
Adjacency list and matrix
领接列表和邻接矩阵是表示图的两种主要的数据结构
- 邻接矩阵是一个二维数组,其中的行和列都代表图中的节点。如果节点i和节点j之间存在一条边,那么矩阵的第i行第j列(和第j行第i列,如果是无向图)的元素就是1(或者是边的权重,如果是加权图),否则就是0。
- 邻接列表:邻接列表是一个一维数组,数组的每个元素都是一个链表,代表一个节点的所有邻居。如果节点i和节点j之间存在一条边,那么节点j就会出现在节点i的链表中(节点i也会出现在节点j的链表中,如果是无向图)。
Diagraph 有向图
如果一个有向图上任意两个点u, v都满足u reaches v,v reaches u,那么这个图是强连接
有向图的cycle示例
如果一个有向图没有cycle,这个有向图是acyclic。
DFS & BFS
深度优先搜索和广度优先搜索的时间复杂度都是O(n+m),n表示图中节点的数量,m表示图中边的数量。因为在搜索过程中,每个节点都需要被访问,每条边也会被检查,因为需要通过边来找到节点的邻居。
DFS使用栈实现,BFS使用队列实现。
DFS实现
void DFS(int vertex, boolean visited[]) {
visited[vertex] = true;
System.out.print(vertex + " ");
Iterator<Integer> it = adjLists[vertex].listIterator();
while (it.hasNext()) {
int adj = it.next();
if (!visited[adj]) DFS(adj, visited);
}
}
void DFS(int vertex) {
boolean visited[] = new boolean[numVertices];
DFS(vertex, visited);
}
BFS实现
void BFS(int vertex) {
boolean visited[] = new boolean[numVertices];
LinkedList<Integer> queue = new LinkedList<>();
visited[vertex] = true;
queue.add(vertex);
while (!queue.isEmpty()) {
int s = queue.poll();
System.out.print(s + " ");
Iterator<Integer> it = adjLists[s].listIterator();
while (it.hasNext()) {
int n = it.next();
if (!visited[n]) {
visited[n] = true;
queue.add(n);
}
}
}
}
两种算法都使用了一个 boolean 数组来追踪哪些顶点已经被访问过。然后,DFS 使用了递归来访问顶点的每个邻居,BFS 使用了一个队列来按照距离顶点的顺序访问邻居。
单源最短路径 & Dijkstra’s algorithm
sssp(single-source shortest path)问题是基于带权重的图。找到从一个顶点到另一个顶点的最短路径,每条边都是带有权重的。
Dijkstra的算法基于广度优先搜索,它考虑了边的权重。
- 在开始时,将源节点的距离设为0,将所有其他节点的距离设为无穷大
- 将所有节点放入一个优先队列(或者最小堆),其中优先级由节点到源节点的距离决定。
- 从优先队列中取出距离最小的节点,对其所有未访问过的邻居进行松弛操作(如果通过当前节点到达邻居的距离小于邻居当前的距离,则更新邻居的距离。)
- 将当前节点标记为已访问,并将其从优先队列中移除。
- 重复上两个步骤,直到优先队列为空,即所有可达的节点都已访问。
细致说下松弛操作:我们检查通过u到v的路径是否比当前从源节点到v的路径更短。也就是说,我们比较d[v]和d[u] + w(u, v)。如果d[u] + w(u, v)更小,那么我们就更新d[v]的值为d[u] + w(u, v)。有点动态规划的思想。
最大流问题和二分图匹配
Ford-Fulkerson algorithm
这是解决最大流问题的算法
最大流问题:有一个有向图,其中每条边都有一定的容量。还有两个特殊的节点:源节点(source)和汇点(sink)。目标是找到一种方式,使得从源节点到汇点的流量最大,同时遵守每条边的容量限制。下面是最大流问题的图。
Ford-Fulkerson algorithm的重要思想
- augmenting paths
- 增广路径:是一条从源点到终点的路径,路径上的所有边的剩余容量都大于零。
- residual networks 残叉网络
- Forward edges 原始网络中存在的边,它们在残差网络中的容量等于原始容量减去当前流量。表示可以在这条边上增加多少流量。
- Backward edges 原始网络中不存在的边,它们在残差网络中表示可以减少多少流量。向后边是原始边的反向边,容量等于原始边的当前流量
- cuts 削减
- 没有增广路径存在时,流量是最大的。
- 一个cut(S, T) 是对图 G = (V, E) 的顶点集 V 的一种划分,其中 V 是顶点集,E 是边集。在这个划分中,S 和 T = V - S 是两个不相交的子集,它们的并集是 V,即每个顶点要么在 S 中,要么在 T 中,且源点 s 属于 S,汇点 t 属于 T。一个cut的容量是所有从 S 到 T 的边的容量之和
Max-Flow/Min-Cut Theorem: Max-Flow的值等于Min-cut的容量
Bipartite graphs & Max matching
Bipartite graphs
在一个二分图中,所有的顶点可以被分为两个不交的集合(我们通常称之为部分或者分区),并且图中的每一条边都连接了一个集合中的顶点和另一个集合中的顶点。也就是说,不存在一条边连接了同一个集合中的两个顶点。
Max matching
一个匹配是图中一组边的集合,满足这组边中的任意两条边都不共享顶点。最大匹配则是包含边数最多的匹配。 常见的经典问题:假设有一组工人和一组任务,每个工人可以完成特定的任务,但每个工人一次只能完成一个任务,每个任务也只能由一个工人完成。这样的问题可以通过寻找二分图的最大匹配来解决。
加密与数论
数论
- 可整除性
- a|b表示a能整除b,b是a的倍数,b=ak。
- 如果 a|b 并且 b|c, 那么 a|c. (transitivity)
- 如果 a|b 并且 a|c, 那么 a|(i · b + j · c). i和j是任意整数
- 如果 a|b 并且 b|a,那么a和b互为相反数。
- 算术基本理论
- 一个质数集合$p$ = {$p_1, p_2, …, p_k$},一个整数集合$e$ = {$e_1, e_2, …, e_k$}
- 任何一个整数m都可以表示成$m$ = $p_1^{e_1}p_2^{e_2}…p_k^{e_k}$
- 最大公约数(GCD)
- gcd(a,b)=1,a和b是relatively prime
- a>0, gcd(a,0)=a or gcd(0,a)=a
- gcd(a,b)=gcd(|a|,|b|),无论ab是正是负。
- gcd(0,0) is undefined.
- The modulo operator and congruences(模和同余)
- 如果 a mod n = b mod n. In this case, a is congruent to b modulo n(a和b对n同余), note a $\equiv$ b (mod n)
- 如果a $\equiv$ b (mod n),意味着a-b=kn
- −10 mod 3 = 2, -10/3 = -4, so -10 - (-4)*3 = 2
- Euclid’s algorithm
- 一种找最大公约数的算法
- 如果$a\ge b > 0$,gcd(a, b) = gcd(b, a mod b)
while b!=0 do (a,b)<-(b,a mod b) return a
加密通信
对称加密
传统加密机制中,Alice和Bob共享一个公钥k。这个公钥是用来加密和解密的,之所以叫对称加密,是因为发出者和接收者使用的是同一个密钥来加密/解密信息。
对称密码中最简单的一种形式是substitution cipher(替换密码)。加密过程:
- 加密:明文M中的每个字符x都通过密钥π映射到对应的字符y。比如,如果π定义为"A变为D,B变为H",那么明文"AB"就会被加密为"DH"。
- 传输:加密后的密文C被发送给接收者。
- 接收者在知道密钥π的情况下可以轻松地解密密文:
- 解密:密文C中的每个字符y都通过π的逆排列$x=π^{−1}(y)$映射回原始的字符x。继续上面的例子,如果接收者知道"A变为D,B变为H",那么他就可以将密文"DH"解密回原始的明文"AB"。
- 缺点:但这很容易被破解。。。
另一种是凯撒密码。明文中的每个字符x被替换成新的字符y,其计算公式为 y = (x + k) mod n。其中:
- n是字母表的大小。例如,如果我们使用英语字母表,那么n就是26,因为英语字母表包含26个字母。
- k是秘密密钥,是一个正整数,并且满足1 ≤ k < n。这个密钥决定了字符替换的位移。例如,如果k = 3,那么字母"A"就会被替换成字母"D",字母"B"替换成"E",依此类推。当到达字母表的末尾时,会从字母表的开头继续替换。
- 缺点:k值有限,非常容易被暴力破解,今天也没人用。。。
一种安全的对称加密(OTP)一次性密码本方案。其工作原理如下:
- 生成密钥:Alice和Bob共享一个随机比特串K,长度至少与他们要发送的消息M一样长。比特串K用于加密和解密的对称密钥。
- 加密:Alice将明文消息M与密钥K进行异或操作($0\oplus0=1\oplus1=0, 0\oplus1=1$),生成密文C。因为K是随机的,所以C也是随机的,没有任何可以用来猜测M或K的模式。
- 传输:密文C被发送给Bob。
- 解密:Bob收到密文C后,他也将C与同样的密钥K进行异或操作,恢复出明文消息M。这是因为任何数值与自身异或两次都会返回原始值。$C\oplus K = (M\oplus K)\oplus K=M\oplus(K\oplus K)=M\oplus0=M$。
- 所以,理论上讲只要密钥K不被拦截窃取,且每个密钥只使用一次,那么密文就无法被破解。
- 缺点:K会非常大,并且只能用一次,很多应用场景被限制住了。我们倾向于可以重复使用并且简短的密钥
非对称加密
基于OTP的需求痛点,公钥加密出现了
- 公钥加密
假设加密函数是E,解密函数是D,消息是M,公钥加密有一下几个性质
- D(E(M)) = M,经加密函数处理后再解密,得到加密前的消息M
- D和E函数都很易于计算。花费太长时间会使很多应用场景失去意义
- 由D推导出E被认为是不可能的,不然每个人都很容易被攻击
- E(D(M)) = M,在一些公钥系统中,这是成立的,但不是所有的公钥系统都满足这个属性。它表明解密后的消息可以再次被加密回到原始消息。这个性质在某些情况下是有用的,比如数字签名,但并不是所有的公钥密码体系都需要(或满足)这个性质。
- 加密函数E也被称为单向函数,即无法通过它推导出D。这也是为什么这种加密方式叫做公钥加密。加密函数是公有的,解密函数E是私有的。这就不需要担心消息发送过程中的安全,因为只要解密函数不被偷走,即使消失被半路拦截也无法被解密。
- RSA加密模式
RSA是最早提出的一种公钥加密算法之一。
主要思想: p和q是两个不同的大质数。令n=pq, $\phi(n)=(p-1)(q-1)$,选择两个数字e和d满足以下条件
- $1<e<\phi(n)$
- $e, \phi(n)$是relatively prime,即$gcd(e, \phi(n))=1$
- $ed\equiv 1 ($ mod $ \phi(n))$
(e, n)这个值对就是公钥,d就是私钥。
RSA加密
- M是一个整数,0<M<n,M是每个字符的ASCII值的拼接,如果大于等于n,就把M拆成几块
- 用公钥e和n来加密M,$C = M^e$ mod $n$
RSA解密
- $M = C^d$ mod $n$
- 证明过程在这里
NP Complete
Hard computational problems
有很多问题难以找到一个有效的算法来解决。但是我们也无法证明出这些问题就是难以解决的,我们只是无法确定是否有算法存在来解决这种问题还是说这种问题就是无法解决的。所谓有效的算法指的是可以在多项式时间内解决所有输入的函数。
0-1背包问题就是一个很典型的NP完全问题,因为其时间复杂度是 O(nW),(n 是物品的数量,W 是背包的容量)。动态规划解法的时间复杂度 O(nW) 被认为是非多项式的,因为 W 是背包容量的具体数值,而不是它的位数(所以O(nW)实际是O(nlogW),整数W用logW位的二进制数字表示。相当于执行了$2^W$次操作,这是一个指数时间的算法)。所以,如果 W 的值增长非常大,那么算法的运行时间会急剧增长。
但是可以在多项式时间内验证一个给定的解是否正确。 这是通过检查给定解的总价值和总重量来完成的。 假设我们有一个可能的解,即一个标识每个物品是否被选择放入背包的向量。我们可以通过以下步骤在多项式时间内验证这个解是否有效:
- 初始化总重量和总价值为0。
- 遍历物品列表,对于每个被选择的物品,将其重量加到总重量,并将其价值加到总价值。
- 最后,我们检查总重量是否超过背包的容量。如果超过,那么这个解是无效的。如果没有超过,那么这个解是有效的,总价值是我们得到的解的价值。
- 这个过程的时间复杂度是 O(n),其中 n 是物品的数量,因此可以在多项式时间内完成。
Hamiltonian Graph
如果一个图是哈密顿图,那么在这个图中就可以找到一条路径,该路径恰好访问图中的每个顶点一次,并且如果这个路径是闭环(即起始和终止于同一顶点)。需要注意的是,确定一个给定的图是否是哈密顿图是一个著名的NP完全问题,意味着没有已知的多项式时间算法可以解决这个问题。
决策/优化问题
- 决策问题(decision problem)的输出要么是yes要么是no。
- 优化问题(optimisation problem)中我们尝试最大或最小化某些函数。
- 一个优化问题通过添加一个参数k就可以转换成决策问题。这个函数的值是否最大(或最小)为k。
- 如果解决一个决策问题很困难,那么与其相关的优化问题也会变的很困难。
一个🌰,还挺助于理解的。
- 优化问题:G是一个连通图,每条边的权重都是整数。求G的最小生成树的权重值
- 决策问题:G是一个连通图,每条边的权重都是整数,现在有一个整数k,是否有这样一个生成树权重值不超过k?
用二分查找的思想找到优化解
- 假设B是0-1背包问题的最大可能收益
- 我们首先问,是否有一个子集能使收益达到至少B/2?
- 如果存在这样的子集,我们继续问,是否有一个子集能使收益达到至少3B/4?
- 如果不存在这样的子集,我们继续问,是否有一个子集能使收益达到至少B/4?
- 这个过程就是不断地在可能的最大收益范围内进行二分查找,逐步缩小搜索范围,直到找到最大可能收益。这个策略的效率在于它利用了二分查找的思想,每次都将搜索范围减半,从而减少了需要检查的可能性。
Complexity Class P
这是一个决策问题的集合,这些决策问题的最坏的情况都可以在多项式时间内被解决。
首先,决策问题是那些输出结果为"是"或"否"的问题,例如“这个图有没有哈密尔顿路径?”或者“这个数是不是素数?”
这段话中的算法A是一个假设存在的算法,它可以在多项式时间内解决一个决策问题。具体来说,如果决策问题s的答案是“是”,那么算法A可以在时间p(|s|)内确定这个结果。这里,|s|表示问题s的“大小”,而p(·)是一个多项式。
这意味着,如果我们能找到这样的算法A,那么我们就能说这个决策问题可以在多项式时间内解决,或者说这个问题在计算复杂性理论中属于P类问题。
Complexity Class P 问题举例
- minimum spanning tree,
- fractional knapsack,
- shortest paths in graphs with non-negative edge weights,
- maximum flows,
- Euler tours, and
- task scheduling.
Efficient Certification
粗浅的说就是对某个问题给出一个解决方案,可以在多项式时间内检查这个解决方案是否正确。证书指的就是给出的解决方案。
Complexity class NP
这个集合包含所有能在多项式时间内被“验证”或“证明”其解的决策问题。NP类由决策问题组成,这些决策问题中都存在Efficient Certification。
P21-41 lec10d