记录一些基础方法
时间序列
可视化三种时间序列
- Brownian motion (stochastic process)
- Lorenz attractor (chaotic system)
- Lotka-Volterra system (deterministic system of differential equations)
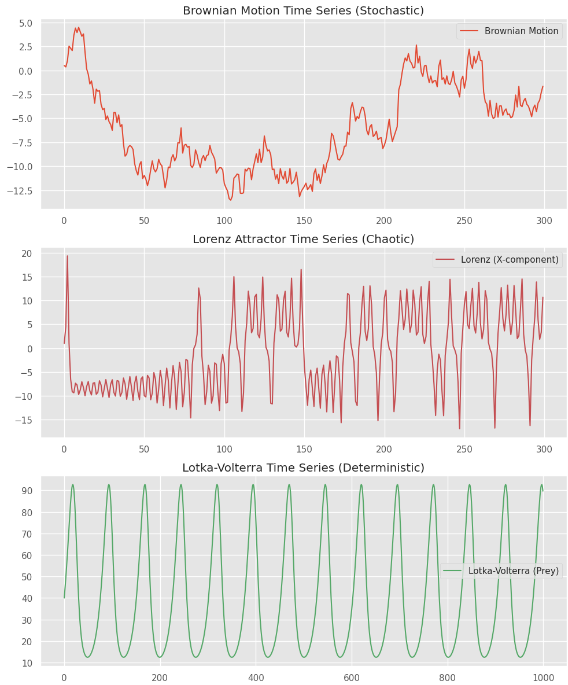
- 随机过程是一种非确定性的过程,即其未来状态依赖于概率分布,无法通过确定的数学公式精确预测。布朗运动(Brownian Motion)是一种典型的随机过程,常见于金融市场、分子扩散等领域。
- 混沌系统是一类确定性但不可预测的系统,即尽管系统是由确定性的方程描述的,但对初始条件极其敏感,导致长期行为难以预测。洛伦兹系统(Lorenz System)是一个经典的混沌系统,最早由 Edward Lorenz 研究气象现象时提出。其特征包括:
- 由确定性方程控制(如微分方程)。
- 对初始条件极其敏感(“蝴蝶效应”)。
- 具有某种结构(如吸引子),但长期行为是不可预测的。
- 确定性系统是完全由数学规则或方程所控制的系统,即 如果初始条件相同,每次运行都会得到相同的结果。洛特卡-沃尔泰拉(Lotka-Volterra)方程描述了捕食者(如狼)和被捕食者(如兔子)种群的动态变化。这类系统的特征包括:
- 未来状态由当前状态唯一决定。
- 没有随机性,系统演化完全可预测。
- 在生物学、物理学、化学等领域有广泛应用。
数据填充技术
这主要用于处理时间序列上的缺失值,主要有三种方法
- Forward Fill: 用前一个已知的值填充当前缺失的值。
- Average of Neighbors: 用缺失值相邻的两个已知值的平均值进行填充,常用于平稳数据。
- Linear Interpolation: 假设缺失值可以沿着相邻观测点的直线关系进行插值。适用于趋势平稳或线性增长/下降的数据。
Preprocessing, scaling & reversing transformations
下面是几种常见的transformation:
- Differencing: Remove trends by looking at changes rather than absolute values.
- Log-Differencing: Stabilize variance and remove trends, often used when dealing with multiplicative trends.
- Normalization (Min-Max): Scale data to [0,1].
- Standardization (Z-score): Transform data to have mean 0 and std 1.
多元时序关系和预测
Granger Casuality Tests
什么是Granger Casuality tests? Granger 因果检验是一种基于时间序列数据的因果推断方法,判断一个时间序列是否“因果地”影响另一个时间序列。
但是Granger因果并不等于真正的因果关系。他只表明时间序列上的因果性。例如,如果$X$领先$Y$发生,并且$X$的历史数据能改善$Y$的预测,那么$X$ Granger因果地导致$Y$,但这不一定是实际的因果关系(可能存在未观察到的第三个变量)。Granger因果的优点是比单纯的correlation更复杂,并且可以给预测能力提供一个检验(通常是基于回归的统计检验)。缺点就是它仍然在假设线性关系,而且Granger因果并不代表真实事件中一定是因果关系。
Transfer Entropy
Transfer Entropy(传递熵) 是一种用于量化时间序列之间信息流动的非线性因果推断方法,常用于检测时间序列变量之间的因果关系。
核心概念
- 信息论基础:Transfer Entropy 基于 香农信息熵 和 条件概率,衡量从一个时间序列到另一个时间序列的信息传递量。
- 非对称性:Transfer Entropy 是有方向的,信息传递可以是:
X → Y(X 影响 Y)- 但
Y → X不一定成立
- 非线性:可以捕捉复杂的非线性因果关系,相比于 Granger 因果检验(基于线性回归),Transfer Entropy 更加灵活。
数学原理
- 假设有两个时间序列 $X$ 和 $Y$:
- $X_t$:时间 $t$ 时刻的 $X$
- $Y_t$:时间 $t$ 时刻的 $Y$
- Transfer Entropy $T_{X \to Y}$ 定义为:
$
T_{X \to Y} = \sum p(y_{t+1}, y_t^{(k)}, x_t^{(l)}) \log \frac{p(y_{t+1} \mid y_t^{(k)}, x_t^{(l)})}{p(y_{t+1} \mid y_t^{(k)})}
$
- $y_t^{(k)}$:表示 $Y$ 在过去 $k$ 个时间步的历史信息。
- $x_t^{(l)}$:表示 $X$ 在过去 $l$ 个时间步的历史信息。
- 核心:如果在已知 $Y$ 自身历史的基础上,加入 $X$ 的历史信息能提高 $Y$ 的未来预测能力,那么 $X$ 向 $Y$ 传递了信息,Transfer Entropy 就是衡量这个“增量”的量。
Transfer Entropy 与 Granger Causality 的区别
| 特性 | Granger Causality | Transfer Entropy |
|---|---|---|
| 假设 | 假设变量之间是线性关系 | 无假设,可以检测非线性因果 |
| 方法 | 基于线性回归进行预测 | 基于信息论和概率分布 |
| 结果 | 输出p 值,判断因果性 | 输出信息传递量,数值越大表示因果性越强 |
| 对称性 | 可能存在对称性(但不总是) | 非对称,能量化方向性 |
| 应用场景 | 经济、金融、时间序列分析 | 神经科学、复杂系统、气候变化分析 |
Transfer Entropy 的优势
- 捕捉非线性关系:在复杂系统中,变量之间往往存在非线性关系,Transfer Entropy 能检测这些关系。
- 适用于非平稳时间序列:时间序列数据常常是非平稳的,Transfer Entropy 在处理这些数据时更灵活。
- 度量因果强度:Transfer Entropy 不仅判断因果方向,还可以量化因果强度,数值越大表示信息流动越强。
- 非对称性:能区分
X → Y和Y → X之间的信息流动,避免了因果“误判”。
Transfer Entropy 的应用
- 神经科学:分析脑区之间的信息传递,理解神经元的相互作用。
- 金融市场:分析不同股票或市场指数之间的信息流动,检测市场的领导效应。
- 气候科学:研究气候系统中不同气候指数(如 ENSO、NAO)之间的信息传递。
- 生态学:分析生态系统中物种之间的相互作用,如捕食者和猎物之间的信息流动。
Linear Regression for Multivariate Forecasting
VAR Model for Multivariate Forecasting
Vector Auto-Regression 模型捕捉多个变量之间的线性相互依存关系。VAR 模型中的每个变量都是系统中所有变量过去值的线性函数。VAR不仅可以同时模拟多个时间序列,而且可以捕捉反馈回路,例如厄尔尼诺/南方涛动如何依赖于大气环流,大气环流又如何依赖于厄尔尼诺/南方涛动等。但是它仍然假设问题是线性的,而且需要静态或非静态差分。还需要估计很多参数,稍有不慎就会导致过度拟合。